_-
Las matemáticas han sido increíblemente eficientes para describir la naturaleza.
Las matemáticas son algo absolutamente fascinante. Y están en todos lados: en las simetrías de los pétalos de las flores, en las conchas de los moluscos, en el patrón que siguen las manchas que tienen en la piel muchos animales, en los hexágonos de los copos de nieve, en la música, en los cristales minerales, en el arte… Vivimos rodeados de matemáticas.
El mexicano José Luis Aragón Vera es un apasionado de esta disciplina.
Director del Centro de Física Avanzada y Tecnología Aplicada de la Universidad Nacional Autónoma de México, este doctor en Física de Materiales por el Centro de Investigación Científica y de Estudios Superiores en Ensenada, Baja California, es experto en cristalografía matemática y en biomatemáticas.
BBC Mundo habló con él en el marco del Hay Festiva Digital Querétaro.
Galileo aseguró hace ya varios siglos que el universo está escrito en el lenguaje de las matemáticas. ¿Es así?
Yo creo que Galileo se dio cuenta de la gran efectividad que tienen las matemáticas para describir los fenómenos naturales, pero yo considero que las matemáticas son una creación nuestra, de la mente humana.
Pienso que las matemáticas son nuestra forma de ver la naturaleza, más que el lenguaje en el que la naturaleza está escrita. Y son creíblemente eficientes, eso sí que es cierto.
Entonces, ¿las matemáticas las inventamos, no las descubrimos?
Así es. Las inventamos nosotros, las creamos nosotros.
Históricamente, las matemáticas nacen por la necesidad de contar y de medir. Pero, poco a poco, comienzan a tener un cambio, y en el siglo XVII empiezan a orientarse más hacia las aplicaciones.
Newton, por ejemplo, inventa el cálculo diferencial integral pensando en un fenómeno físico como es la gravitación.
Y a finales del siglo XIX hay un cambio notable en las matemáticas: se convierten en un conjunto de objetos abstractos y de reglas para manejar esos objetos. Y esas reglas las inventan los matemáticos, son creación de ellos.
Pero si por ejemplo los pétalos de las flores y las manchas en la piel de algunos animalesse ordenan siguiendo reglas matemáticas, y tantas cosas que nos rodean responden a leyes matemáticas, ¿no podría ser que las matemáticas estuvieran allí y que nosotros las descubriéramos?
Eso nos podría llevar a una discusión filosófica. Mi opinión, y la de otros muchos, es que nosotros creamos las matemáticas. Y esa creación nuestra ha sido increíblemente eficiente para describir la naturaleza.
Hay un artículo que el físico Eugene Wigner escribió en los años 30 y cuyo título ya dice mucho: "La irrazonable efectividad de las matemáticas para describir las ciencias naturales".
En él, Wigner llega a la conclusión de que no se sabe por qué las matemáticas son tan eficientes. Es un artículo muy famoso que se ha escrito, reescrito, discutido… Pero sigue sin haber una conclusión.
Las matemáticas han sido increíblemente eficientes para describir la naturaleza.
¿Todo lo que nos rodea se puede explicar con el lenguaje matemático?
Muchas cosas sí: todo lo que son fenómenos naturales, también el arte, la música… No hay nada más matemático que la música.
Sin embargo, hay cuestiones como los fenómenos sociales, donde es muy difícil que las matemáticas funcionen, porque intervienen muchos factores.
Piense por ejemplo en predecir el comportamiento de la bolsa de valores: con que uno de los compradores se asuste y venda, se puede desencadenar una venta en cascada y que caiga la bolsa.
Hay modelos matemáticos que tratan de predecir esas cosas, pero son modelos que contienen en sí mismos esa impredecibilidad.
Las emociones son algo donde las matemáticas no suelen funcionar. ¿Es posible que en el futuro, con el desarrollo de la inteligencia artificial, las emociones se puedan formular con patrones matemáticos?
Es posible que sí. Con respecto a la inteligencia artificial, hay dos corrientes.
Por un lado, está la llamada inteligencia artificial fuerte, que argumenta que los procesos de pensamiento y los mecanismos de las emociones responden a algoritmos, y si son algoritmos una computadora los va a poder hacer, por muy complicados que sean.
Pero hay otra corriente, encabezada entre otros por Roger Penrose, un físico de Cambridge, que sostiene que no, que los pensamientos y los sentimientos no responden a un algoritmo, que hay fenómenos adicionales y que por ello una computadora nunca llegará a tener sentimientos como un ser humano.
Hay dos corrientes y mucho debate.
¿Y usted con cuál de esas dos corrientes se queda?
Con la que piensa que las computadoras nunca van a llegar a tener sentimientos.
¿Legará la inteligencia artificial a tener sentimientos o solamente entenderlos?
El mundo que tenemos hoy en día, ¿no existiría sin las matemáticas?
Si no hubiéramos sido capaces de inventar las matemáticas no tendríamos el nivel de progreso que tenemos ahora.
En estos momentos está pasando una cosa muy curiosa.
En el mundo moderno, con la alta tecnología que tenemos, los que están empezando a tomar el control son los matemáticos.
A las empresas les interesa mucho todo lo que son redes sociales y manejo de cantidades enormes de datos, porque a través de las búsquedas en internet y de las ventas pueden saber lo que nos gusta, cuáles son nuestros patrones de compra y así saben qué vendernos.
Incluso a través de las matemáticas se puede llegar a influir en las opiniones: las noticias falsas, las fake news, son creadas por algoritmos matemáticos muy complejos que imitan la manera de escribir de las personas.
Y detrás de todo eso está el conocimiento matemático, y los matemáticos están cada vez más cotizados.
Si miramos atrás, vemos que cuando llegó el desarrollo de la energía nuclear los profesionales más cotizados eran los físicos. Después llegó el boom de la ingeniería genética, y los más cotizados pasaron a ser los biólogos. Y ahora son los matemáticos.
Arte abstracto Getty
Ha habido artistas muy famosos que han tenido mucho gusto por las matemáticas y han metido en sus obras de arte conceptos matemáticos"
Si no hubiéramos inventado las matemáticas, ¿cómo sería el mundo en estos momentos?
Pues seguiríamos teniendo creencias religiosas para explicar lo que vemos, no tendríamos grandes teorías sobre cómo funcionan las cosas.
Sin las matemáticas no podríamos explicar el mundo natural como lo hemos explicado hasta ahora.
¿Las matemáticas son la perfección? Se lo pregunto porque en la naturaleza, cuando hay patrones matemáticos generan algo que parece perfecto…
Lo que hay detrás de las matemáticas siempre es el rigor lógico, y el rigor lógico siempre da esa sensación, no sólo de perfección sino también estética. Es bello, muy bello. Por eso, las matemáticas y el arte viven en concubinato.
El arte es algo que nace de las emociones, ¿dónde están las matemáticas en el arte?
En las artes plásticas hay geometría. La geometría se cree que nace en Babilonia en el año 3000 a.C., aunque algunas teorías dicen que nació mucho antes, desde que los seres humanos tuvieron la necesidad de adornar sus cuerpos para ritos religiosos o de cortejo.
Si aceptamos eso, ahí ya se ve que la geometría y la estética están muy relacionadas.
Pero yo creo que los primeros en darse cuenta de la relación entre la geometría y el arte son los griegos.
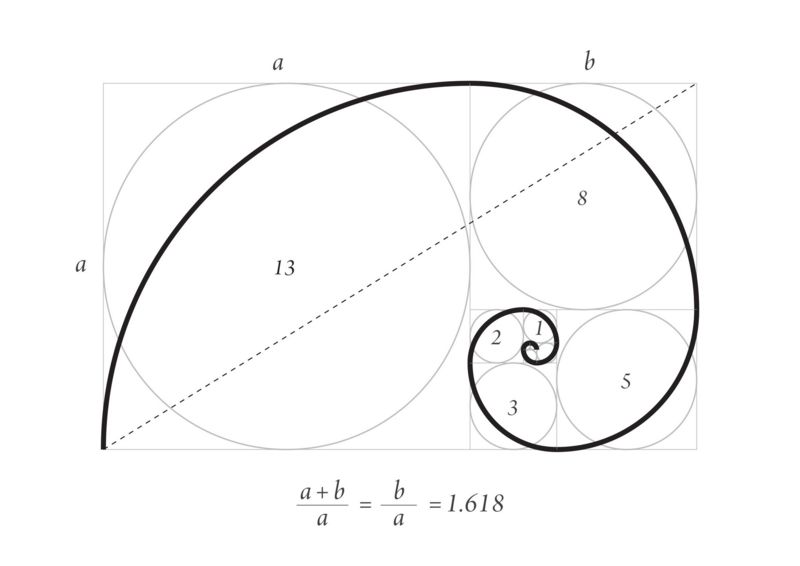
La proporción áurea, por ejemplo, es un número irracional que vale aproximadamente 1,618 y que tiene propiedades matemáticas muy notables.
Proporción áurea
FUENTE DE LA IMAGEN,GETTY IMAGES
La proporción áurea también es llamada la "divina proporción".
Los griegos fueron los primeros que se dieron cuenta de que con ella se pueden formar figuras geométricas muy placenteras.
Por qué son placenteras no se sabe, pero lo son: si, por ejemplo, formamos un rectángulo en el que un lado vale 1 y el otro la proporción áurea, 1,618, y otros muchos rectángulos de distintas medidas y se los enseñamos a niños y adultos, casi siempre se quedan con el que tiene la proporción áurea.
El escultor y arquitecto griego Fidias utilizó la proporción áurea para el Partenón, y Leonardo Da Vinci ilustró un libro muy famoso de Luca Pacioli sobre "la divina proporción", que es como llamaba a la proporción áurea.
Ha habido muchos artistas y creadores que la han utilizado, hasta llegar al arquitecto Le Corbusier: su edificio de la ONU en Nueva York tiene justo esas proporciones.
¿A los artistas les gustan entonces las matemáticas?
Sí. Ha habido artistas muy famosos que han tenido mucho gusto por las matemáticas y han metido en sus obras de arte conceptos matemáticos más avanzados: Durero, Man Ray, Kandinsky, Escher…
Siguiendo con el tema de la perfección… Los matemáticos hablan de círculos y de triángulos perfectos, de números compuestos de unidades perfectamente iguales entre sí, de números irracionales que no tienen fin… Pero nada de eso existe en la realidad, ¿verdad?
Tiene toda la razón. La proporción áurea, por volver a ella, es exactamente 1+√5/2, y ese es un número irracional que vale 1,618034… etcétera, etcétera.
Obviamente, nunca vamos a tener un rectángulo con esa proporción exactamente, lo que se obtiene una proporción aproximada. Pero eso funciona muy bien, la ciencia también se basa en aproximaciones que funcionan.
Cuando Newton propuso la teoría de la gravitación y que la Tierra atraía a la Luna calculó cuál sería la órbita alrededor de la Tierra suponiendo que ambas son esferas, cuando en realidad no lo son.
Pero si hubiera hecho los cálculos teniendo en cuenta que una tiene forma de naranja y la otra está aplastada por un lado nunca hubiera llegado a su teoría.
Todo se basa en aproximaciones. Las matemáticas dan cantidades exactas y perfectas, pero al aplicarlas se hace con aproximaciones que funcionan muy bien.
Newton se basó en las matemáticas, pero tuvo que hacer aproximaciones para generar su teoría de la gravedad.
¿Qué nos queda por saber del mundo de las matemáticas?
Nos quedan muchas cosas, pero es muy difícil predecir qué nuevas reglas se van a proponer, qué nuevas áreas se van a crear.
¿A usted qué le gustaría descubrir?
El gran reto que hay ahora es desarrollar unas matemáticas que puedan explicarnos cosas como el caos.
Hay fenómenos naturales sobre los que no podemos hacer predicciones más allá de tres o cuatro días, como por ejemplo el clima. Y lo que no sabemos es si la naturaleza en realidad es así o si no tenemos las matemáticas adecuadas para hacer mejores predicciones.
Muchos fenómenos naturales no son lineales, y aún no hay matemáticas para tratarlos. Me gustaría descubrir eso: unas matemáticas para los fenómenos no lineales.
Hubo un matemático ruso muy famoso, Andrei Kolmogorov, que estudió en concreto la turbulencia, un fenómeno no lineal muy complejo, hasta el punto de que hay una universidad en Canadá que lo considera uno de los problemas del siglo y ofrece un millón de dólares a quien lo resuelva.
Kolmogorov atacó esos problemas, pero se dio cuenta de que no podía llegar muy lejos con las matemáticas que había, y dijo que hacía falta el golpe de un genio, crear las matemáticas adecuadas para esos fenómenos tan complicados.
Andrei Kolmogorov concluyó que con las matemáticas existentes no podía resolver algunos fenómenos no lineales.
¿Los matemáticos tienen otra manera de pensar?
Yo creo que sí.
Cuando doy clases de matemáticas yo siempre le insisto a mis estudiantes que a mí no me importa mucho si al rato no se acuerdan de la fórmula tal, o de cómo se diagonaliza una matriz o qué es la independencia lineal.
Mi objetivo es que aprendan a pensar como piensan los matemáticos: con consistencia lógica, encadenando razonamientos, buscando siempre consecuencias a través de la lógica, etc.
¿Y esa forma particular de pensar la trasladan a todas las esferas de la vida?
Sí. Hay en ese sentido una anécdota muy conocida: durante la II Guerra Mundial querían blindar los aviones para evitar que les hicieran daño al dispararles. Pero blindar un avión entero es imposible, pesaría mucho.
Un grupo de ingenieros, generales y dos matemáticos se pusieron a pensar y vieron que la mayoría de los aviones tenían más impactos en el fuselaje, así que pensaron que lo mejor sería blindar esa parte.
Pero los matemáticos preguntaron dónde recibían menos impactos los aviones atacados. Les respondieron que en el motor, y decidieron que eso era lo que había que blindar, pues si los aviones mostraban pocos impactos en el motor, significaba que los que recibían disparos ahí no habían podido volver.
Esa es una manera de pensar matemática.
¿Las matemáticas son entonces una forma de vivir?
Son una forma de pensar, y eso evidentemente impacta también en tu forma de vivir.
Arte abstracto Getty
Hay muchos modelos matemáticos que han intentado predecir el comportamiento de la pandemia… creo que son muy importantes, aunque también creo que han sido bastante ignorados"
¿Y qué tal se llevan las matemáticas con las emociones?
Suelen tener una relación muy complicada. Las emociones son poco racionales para la manera de ver las cosas de los matemáticos. Muchos matemáticos muy famosos han tenido un comportamiento complicado.
El último conocido es Grigori Perelman, que logró resolver la famosa conjetura de Poincaré, uno de los problemas del milenio.
Había una recompensa de un millón de dólares a quien la resolviera, y también le ofrecieron la medalla Fields (el más importante galardón que puede recibir un matemático), y no quiso ninguna de las dos cosas. Se quedó en su casa tocando el violín.
Hoy en día hay más mujeres destacándose en las matemáticas.
¿Qué hay de matemáticas en esta pandemia que estamos viviendo?
Muchísimo. Hay muchos modelos matemáticos que han intentado predecir el comportamiento de la pandemia, que proponen modelos sobre cómo evitar su propagación…
Hay muchos modelos y yo creo que son muy importantes, aunque también creo que han sido bastante ignorados.