Ni la matemática ni la física moderna existirían sin el álgebra. No habría computadoras sin algoritmos, ni química sin alcalinos", dijo el físico teórico Jim Al-Khalili.
El profesor de la Universidad de Surrey realizó el documental de la BBC "Ciencia e Islam".
"El lenguaje de la ciencia moderna todavía tiene muchas referencias a sus raíces árabes", señaló en el programa.
"Desde el siglo XII hasta el XVII, académicos europeos hacían referencia con regularidad a textos islámicos del pasado".
Y saca una copia de Liber Abbaci de Leonardo de Pisa, mejor conocido como Fibonacci, quien se convertiría en el primer gran matemático medieval de Europa.
"Lo que es fascinante es que en la página 406 hay una referencia a un texto antiguo llamado Modum algebre et almuchabale y en el margen está escrito el nombre Maumeht, la versión latinizada del nombre árabe Mohammed", indica Al-Khalili.
Se trataba de Abu Abdallah Muḥammad ibn Mūsā al-Jwārizmī, conocido en español como Al-Juarismi, quien vivió aproximadamente entre los años 780 y 850.
Al-Juarismi describió la idea revolucionaria de que se puede representar cualquier número que desee con solo 10 sencillos símbolos.
El gran matemático, que emigró de Persia oriental a Bagdad, le dio a Occidente los números y el sistema decimal. A menudo se le conoce como el padre del álgebra.
"Muchas de las ideas que anteriormente se pensaba que habían sido conceptos nuevos y brillantes gracias a los matemáticos europeos de los siglos XVI, XVII y XVIII, ahora se sabe que fueron desarrolladas por matemáticos árabes/islámicos unos cuatro siglos antes", escribieron John Joshep O'Connor y Edmund Frederick Robertson, de la Universidad St. Andrews, en Reino Unido.
"En muchos aspectos, las matemáticas que se estudian hoy tienen un estilo mucho más cercano al de la contribución árabe/islámica que a la de los griegos".
Ha habido grandes matemáticos del mundo árabe e islámico a lo largo de la historia. Estos son tres de ellos.
Al-Batani
Para Juan Martos Quesada, profesor jubilado y exdirector del departamento de Estudios Árabes e Islámicos de la Universidad Complutense de Madrid, una de las principales contribuciones de los matemáticos árabes "fue rescatar la ciencia griega y la latina con sus traducciones".
Jim Al-Khalili realizó el documental de la BBC "Ciencia e Islam".
Pero también recuperaron lo mejor de la ciencia desarrollada por los indios.
"La gran importancia de Al-Batani es que logró unir la astronomía y las matemáticas y hacer un mismo campo de estudio", le indicó Martos Quesada a BBC Mundo.
"Aplicó muchas fórmulas matemáticas a la astronomía. Por ejemplo, determinó con una gran precisión el año solar en 365 días, lo cual fue un gran logro, pues estamos hablando de finales del siglo IX y principios del X".
"Con respecto a los equinoccios, los estudió y halló que había errores en las cuentas que había hecho Ptolomeo y eso sirvió para perfeccionar toda la herencia griega de Ptolomeo que recibieron los matemáticos árabes".
Además introdujo una serie de relaciones trigonométricas.
Al-Khalili visitó la Universidad de Padua, en Italia, y vio uno de los libros más importantes de la historia de la ciencia: De revolutionibus orbium coelestium, publicado en 1543 por Nicolás Copérnico.
"La importancia de este libro es enorme. En él, Copérnico argumenta por primera vez, desde la antigüedad griega, que todos los planetas, incluyendo la Tierra, giran alrededor del sol".
"Muchos historiadores lo califican como el iniciador de la revolución científica europea".
Monumento a Nicolás Copérnico en Polonia.
Copérnico cita a Machometi Aracenfis, que es el gran Al-Battānī.
"Es una gran revelación para mí que explícitamente mencione a un musulmán del siglo IX, que le proveyó de una gran cantidad de información sobre sus observaciones".
Al-Batani, nació en 858 cerca de Urfa, Siria, y murió en 929, en Irak.
"Copérnico usó extensamente las observaciones de Al-Batani sobre la posición de los planetas, el sol, la luna, las estrellas".
Jaime Coullaut Cordero, profesor de Estudios Árabes e Islámicos de la Universidad de Salamanca, habló con BBC Mundo sobre Ibn Al-Shatir, un astrónomo y matemático que nació en Damasco alrededor del año 1304.
"Fue poco conocido en Occidente porque sus obras no se tradujeron al latín".
Sin embargo, cuenta que en los años 80, "unos investigadores descubrieron los modelos planetarios de Ibn Al-Shatir y se dieron cuenta de que eran iguales que los modelos propuestos por Copérnico, unos cuantos siglos después".
Alhacén
Shaikh Mohammad Razaullah Ansari, profesor emérito de Física de la Universidad Musulmana de Aligarh, en India, escribió un artículo para la página de la UNESCO sobre un erudito árabe de los siglos X y XI que se dedicó, no sólo a las matemáticas, sino también a la física, mecánica, astronomía, filosofía y medicina.
Se trata del gran Abū Ali al-Ḥasan Ibn al-Haytham al-Baṣrī, conocido en Occidente como Alhazen y, en español, como Alhacén.
Nació en el año 965 en Irak y murió en 1040 en Egipto.
Formó parte de los famosos científicos de El Cairo y fue llamado el "Segundo Ptolomeo" por los eruditos árabes.
Es considerado el padre del método científico moderno.
El primer científico de verdad
Desarrolló la metodología de "la experimentación como otra forma de probar la hipótesis o premisa básica", indica Razaullah Ansari.
Martos Quesada destaca sus contribuciones a los principios de la óptica.
De hecho, según Razaullah Ansari, su obra más famosa fue sobre la óptica: "Kitab fi al-Manaẓir, en latín Opticae Thesaurus, que fue traducida de forma anónima en los siglos XII y XIII".
Tabla de 1882 que ilustra el desarrollo de los números.
Son siete volúmenes en los que estudió de forma experimental y matemática las propiedades de la luz.
Pero también fue un gran matemático, como explica Ricardo Moreno, autor y profesor asociado en la Facultad de Matemáticas de la Universidad Complutense en la página del Centro Virtual de Divulgación de las Matemáticas.
"Fue uno de los primeros matemáticos árabes que abordó con éxito ecuaciones de grado superior al segundo, al resolver geométricamente una de tercero que, más de mil doscientos años antes, había planteado Arquímedes en su obra 'Sobre la esfera y el cilindro'".
En el campo de la teoría de los números, Alhacén hizo una contribución importante con su trabajo sobre los números perfectos.
También hizo aportes en la geometría elemental e investigó casos específicos de los teoremas de Euclides.
Abu Kamil
Ricardo Moreno señala que la muerte de Al-Juarismi "coincidó aproximadamente con el nacimiento en Egipto de Abu Kamil ibn Aslam ibn Mohammed, llamado el calculista egipcio".
"Vivió ochenta años y nos dejó numerosas obras matemáticas. Entre ellas un tratado de álgebra, cuyo original árabe se ha perdido, pero del que nos han llegado dos traducciones, una latina y otra hebrea".
"Las ecuaciones de segundo grado las resuelve geométricamente, como su predecesor de Bagdad, pero se apoya más directamente en los Elementos".
Según una breve biografía de O'Connor y Robertson, es muy poco lo que se sabe de la vida de Abu Kamil.
Pero lo suficiente para entender su rol en el desarrollo del álgebra.
"Kamil fue uno de los sucesores inmediatos de Al-Juarismi", indican los autores.
De hecho, el mismo Kamil destaca el papel de Al-Juarismi como el "inventor del álgebra".
"Sin embargo, hay otra razón para la importancia de Abu Kamil, y es que su trabajo fue la base de los libros de Fibonacci", señalan O'Connor y Robertson.
"Kamil no sólo es importante en el desarrollo del álgebra árabe, sino que, a través de Fibonacci, también tiene una importancia fundamental en la introducción del álgebra en Europa".
https://www.bbc.com/mundo/noticias-60715978
Mostrando entradas con la etiqueta números. Mostrar todas las entradas
Mostrando entradas con la etiqueta números. Mostrar todas las entradas
lunes, 21 de marzo de 2022
viernes, 22 de enero de 2021
Qué números usaban los antiguos griegos cuando hacían sus asombrosos descubrimientos
Tales de Mileto explicó el solsticio y el equinoccio, predijo eclipses e inventó la geometría abstracta.
Eudoxo de Cnido, además de ser el padre de la astronomía matemática, ideó una teoría de la proporción, que permitió números irracionales, un concepto de magnitud y un método para encontrar áreas y volúmenes de objetos curvilíneos.
Hiparco produjo una tabla de acordes, una tabla trigonométrica temprana.
Euclides escribió un libro de texto sobre álgebra, teoría de números y geometría que aún es relevante.
Aristóteles estimó el tamaño del globo terráqueo; Pitágoras fue el primer matemático puro; ¡Y qué decir de Arquímedes de Siracusa!
Los helenos de la Antigüedad nos dejaron una miríada de logros matemáticos, pero, ¿sabes qué números usaban para hacer tales maravillas?
Palitos y algo más
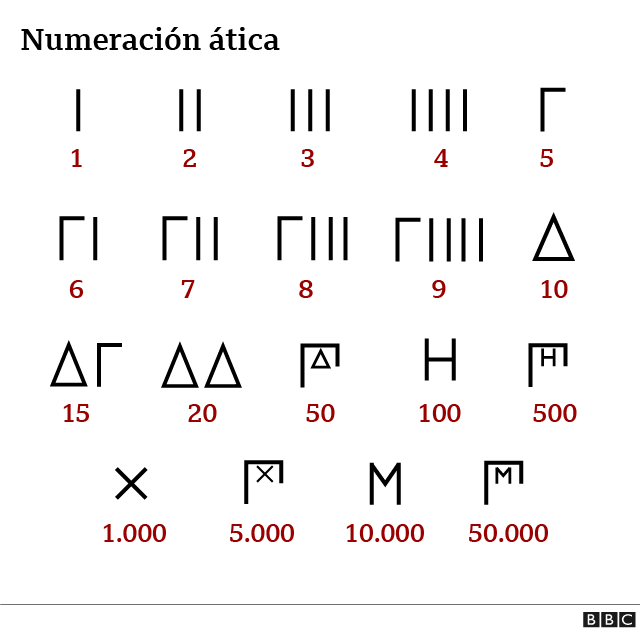
Uno de los sistemas numéricos que se utilizaron en la Antigua Grecia fue la numeración ática, también conocida numerales herodiánicos, pues fueron descritos por primera vez en un manuscrito del siglo II del gran gramático Herodiano.
Pero tienen un tercer nombre que indica cómo eran: números acrofónicos, llamados así porque los signos utilizados para representar el 5 y los múltiplos de 10 eran tomados de las primeras letras del nombre de los números.
Es decir, por ejemplo, X era el símbolo del número 1.000 pues la palabra para mil era Χιλιοι.
Números como 50, 500, 5.000 y 50.000 se formaban usando combinaciones multiplicativas del signo para 5 y los otros signos.
Números áticos
Basar su primer sistema numérico en las iniciales de los nombres de los números no era raro pues en las civilizaciones tempranas se solían escribir las cifras más grandes con letras así que abreviarlas de esa manera era un paso natural.
Por qué los antiguos griegos pensaban que las matemáticas eran un regalo de los dioses
El valor de las letras
La numeración ática fue reemplazada por los números 'jónicos', y para el siglo III a.C. ya eran utilizados regularmente en la escritura griega.
El otro nombre con el que se los conoce nos dice cómo eran: sistema de numerales alfabéticos, es decir, que lo que hicieron fue darles valores a las letras del alfabeto.
¿Notaste que faltan unos números?
Eudoxo de Cnido, además de ser el padre de la astronomía matemática, ideó una teoría de la proporción, que permitió números irracionales, un concepto de magnitud y un método para encontrar áreas y volúmenes de objetos curvilíneos.
Hiparco produjo una tabla de acordes, una tabla trigonométrica temprana.
Euclides escribió un libro de texto sobre álgebra, teoría de números y geometría que aún es relevante.
Aristóteles estimó el tamaño del globo terráqueo; Pitágoras fue el primer matemático puro; ¡Y qué decir de Arquímedes de Siracusa!
Los helenos de la Antigüedad nos dejaron una miríada de logros matemáticos, pero, ¿sabes qué números usaban para hacer tales maravillas?
Palitos y algo más
Uno de los sistemas numéricos que se utilizaron en la Antigua Grecia fue la numeración ática, también conocida numerales herodiánicos, pues fueron descritos por primera vez en un manuscrito del siglo II del gran gramático Herodiano.
Pero tienen un tercer nombre que indica cómo eran: números acrofónicos, llamados así porque los signos utilizados para representar el 5 y los múltiplos de 10 eran tomados de las primeras letras del nombre de los números.
Es decir, por ejemplo, X era el símbolo del número 1.000 pues la palabra para mil era Χιλιοι.
Números como 50, 500, 5.000 y 50.000 se formaban usando combinaciones multiplicativas del signo para 5 y los otros signos.
Números áticos
En este sistema todavía se ven los vestigios de otro más primitivo, que también había sido usado por las culturas que les precedieron -babilonios, egipcios y fenicios- y que consistía en pintar una línea vertical por cada unidad hasta el 9 (aquí todavía lo ves en los signos del 1 al 4).
Basar su primer sistema numérico en las iniciales de los nombres de los números no era raro pues en las civilizaciones tempranas se solían escribir las cifras más grandes con letras así que abreviarlas de esa manera era un paso natural.
Por qué los antiguos griegos pensaban que las matemáticas eran un regalo de los dioses
El valor de las letras
La numeración ática fue reemplazada por los números 'jónicos', y para el siglo III a.C. ya eran utilizados regularmente en la escritura griega.
El otro nombre con el que se los conoce nos dice cómo eran: sistema de numerales alfabéticos, es decir, que lo que hicieron fue darles valores a las letras del alfabeto.
Lo que pasa es que el alfabeto griego clásico tenía 24 letras, pero necesitaban 27 símbolos, así que aprovecharon 3 letras más antiguas que han caído en desuso:
digamma (Ϝ) o stigma (ϛ) para el 6
qoppa (ϙ) para el 90.
sampi (Ϡ) para el 900.
En la siguiente imagen puedes ver números griegos en un manuscrito bizantino del héroe de Alejandría Metrika.
La primera línea contiene el número "͵θϡϟϛ δʹ ϛʹ" -es decir, "9.996 + 1⁄4 + 1⁄6"- en el que están todos los símbolos numéricos especiales: sampi (ϡ), koppa (ϟ) y estigma (ϛ).
Números griegos
Entonces, cada letra representaba un número, y la combinación de ellas permitía representar todos los números... hasta 999, lo cual, te imaginarás, era un gran inconveniente para matemáticos tan ilustres.
Se tuvieron que crear más símbolos para superar el problema.
Un apóstrofe, en la parte superior o inferior a la izquierda de los símbolos del 1 al 9 los convertía en los números entre 1.000 y 9.000.
Con eso llegaban a 9.999.
Para ir más lejos, se valieron del símbolo para la miríada de 10.000 -M- al que le ponían otro arriba que indicara por cuánto había que multiplicarla.
Por ejemplo: si querías expresar 20.000, escribías M con una ß (beta = 2) encima.
Ejemplo de cómo se escribe 123.000
Y cuando los números se volvían muy grandes, escribían el pequeño número que iba arriba antes de la M, como hizo el astrónomo y matemático Aristarco de Samos cuando quiso registrar la cifra de 71.755.875:
Ejemplo
Los números se escribían generalmente de izquierda a derecha, aunque se conocen inscripciones de derecha a izquierda y bustrofedón (es decir, un reglón en una dirección y el siguiente en la otra).
No había ningún signo de cero o similar, pues no era necesario; el sistema era aditivo en lugar de uno basado en la posición o el valor posicional.
No obstante, en algún momento un grupo reducido de científicos usaron un cero como signo de puntuación con fines puramente de notación, no como un número. El símbolo, cuando no era simplemente un espacio en blanco, era ο para "obol" (una moneda de menor valor).
¿Éste o el otro?
Entre el 475 a. C. y el 325 a. C., los números jónicos dejaron de utilizarse en favor de la numeración ática.
Pero desde finales del siglo IV a. C. en adelante, los números alfabéticos se convirtieron en el sistema preferido en todo el mundo de habla griega.
Fueron utilizados hasta la caída del Imperio Bizantino en el siglo XV (y aún se usan ocasionalmente en la actualidad).
https://www.bbc.com/mundo/noticias-55478059
digamma (Ϝ) o stigma (ϛ) para el 6
qoppa (ϙ) para el 90.
sampi (Ϡ) para el 900.
En la siguiente imagen puedes ver números griegos en un manuscrito bizantino del héroe de Alejandría Metrika.
La primera línea contiene el número "͵θϡϟϛ δʹ ϛʹ" -es decir, "9.996 + 1⁄4 + 1⁄6"- en el que están todos los símbolos numéricos especiales: sampi (ϡ), koppa (ϟ) y estigma (ϛ).
Números griegos
Entonces, cada letra representaba un número, y la combinación de ellas permitía representar todos los números... hasta 999, lo cual, te imaginarás, era un gran inconveniente para matemáticos tan ilustres.
Se tuvieron que crear más símbolos para superar el problema.
Un apóstrofe, en la parte superior o inferior a la izquierda de los símbolos del 1 al 9 los convertía en los números entre 1.000 y 9.000.
Con eso llegaban a 9.999.
Para ir más lejos, se valieron del símbolo para la miríada de 10.000 -M- al que le ponían otro arriba que indicara por cuánto había que multiplicarla.
Por ejemplo: si querías expresar 20.000, escribías M con una ß (beta = 2) encima.
Ejemplo de cómo se escribe 123.000
Y cuando los números se volvían muy grandes, escribían el pequeño número que iba arriba antes de la M, como hizo el astrónomo y matemático Aristarco de Samos cuando quiso registrar la cifra de 71.755.875:
Ejemplo
Los números se escribían generalmente de izquierda a derecha, aunque se conocen inscripciones de derecha a izquierda y bustrofedón (es decir, un reglón en una dirección y el siguiente en la otra).
No había ningún signo de cero o similar, pues no era necesario; el sistema era aditivo en lugar de uno basado en la posición o el valor posicional.
No obstante, en algún momento un grupo reducido de científicos usaron un cero como signo de puntuación con fines puramente de notación, no como un número. El símbolo, cuando no era simplemente un espacio en blanco, era ο para "obol" (una moneda de menor valor).
¿Éste o el otro?
Entre el 475 a. C. y el 325 a. C., los números jónicos dejaron de utilizarse en favor de la numeración ática.
Pero desde finales del siglo IV a. C. en adelante, los números alfabéticos se convirtieron en el sistema preferido en todo el mundo de habla griega.
Fueron utilizados hasta la caída del Imperio Bizantino en el siglo XV (y aún se usan ocasionalmente en la actualidad).
https://www.bbc.com/mundo/noticias-55478059
lunes, 5 de octubre de 2015
Suscribirse a:
Entradas (Atom)
Entradas
