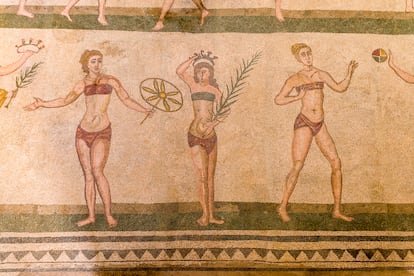Esta es la historia de un libro perdido que podría haber cambiado la historia del mundo. Perdido por más de dos milenios, contiene las ideas de una de las mentes más impresionantes de todos los tiempos.
Y pasarían muchos siglos antes de que otras mentes lograran llegar tan lejos como esa.
Todo comenzó en Siracusa, Sicilia, Magna Grecia, en el año 287 a.C., cuando nació Arquímedes, un genio extraordinario para quien la frase "adelantado a su época" parece haber sido hecha.
"No hay otro matemático en la Antigüedad, ni tampoco en la historia, que se acerque a Arquímedes", declaró Chris Rorres, profesor emérito de Matemáticas de la Universidad Drexel de Pensilvania, EE.UU., en conversación con la BBC cuando el manuscrito fue recuperado.
Arquímedes es aquel hombre que gritó "¡Eureka!" en la bañera.
Estaba tratando de resolver un problema con una corona de oro del rey.
El monarca sospechaba que el orfebre que la había fabricado le había mezclado plata, que era más barata.
La corona pesaba lo indicado, pero como la plata es más ligera que el oro, la pregunta era: ¿sería más grande de lo que habría sido si estuviera hecha de oro puro?
Se cuenta que cuando Arquímedes se metió en la tina y notó que cuanto más se sumergía, más agua se salía de la bañera; se dio cuenta de que podía establecer el volúmen de la corona sumergiéndola en un recipiente con agua y midiendo cuánto líquido se desplazaba.
Dicen que estaba tan emocionado por el descubrimiento que inmediatamente salió de su baño y corrió desnudo por las calles de Siracusa gritando la palabra griega para "lo he descubierto".
Y pasarían muchos siglos antes de que otras mentes lograran llegar tan lejos como esa.
Todo comenzó en Siracusa, Sicilia, Magna Grecia, en el año 287 a.C., cuando nació Arquímedes, un genio extraordinario para quien la frase "adelantado a su época" parece haber sido hecha.
"No hay otro matemático en la Antigüedad, ni tampoco en la historia, que se acerque a Arquímedes", declaró Chris Rorres, profesor emérito de Matemáticas de la Universidad Drexel de Pensilvania, EE.UU., en conversación con la BBC cuando el manuscrito fue recuperado.
Arquímedes es aquel hombre que gritó "¡Eureka!" en la bañera.
Estaba tratando de resolver un problema con una corona de oro del rey.
El monarca sospechaba que el orfebre que la había fabricado le había mezclado plata, que era más barata.
La corona pesaba lo indicado, pero como la plata es más ligera que el oro, la pregunta era: ¿sería más grande de lo que habría sido si estuviera hecha de oro puro?
Se cuenta que cuando Arquímedes se metió en la tina y notó que cuanto más se sumergía, más agua se salía de la bañera; se dio cuenta de que podía establecer el volúmen de la corona sumergiéndola en un recipiente con agua y midiendo cuánto líquido se desplazaba.
Dicen que estaba tan emocionado por el descubrimiento que inmediatamente salió de su baño y corrió desnudo por las calles de Siracusa gritando la palabra griega para "lo he descubierto".

Así se dice en griego.
No sabemos si los ciudadanos de Sicilia alguna vez vieron el cuerpo desnudo de Arquímedes, pero la verdad sobre la corona del rey fue revelada: el orfebre había sido deshonesto y Arquímedes había resultado ser un buen detective.
Durante su vida, Arquímedes se hizo famoso por sus inventos y temido por sus armas de guerra.
El rey lo nombró consejero militar y le encargó la defensa de la ciudad.
Pero es a través de sus matemáticas que se revela su verdadero genio.
3.14159265358979323846...
Fue a él a quien se le ocurrió un valor para π, vital para calcular el área de un círculo, uno de los componentes básicos de la ciencia.
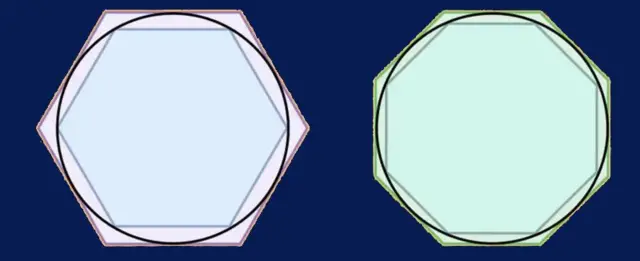
Lo hizo valiéndose de polígonos, pues su perímetro se puede calcular dado que sus lados son rectos.
Comenzó poniendo un hexágono dentro del círculo y otro fuera. Luego, fue agregando más y más lados hasta tener 96.
La idea era hacer que los polígonos se acercaran cada vez más al perímetro del círculo, pues eso le daría un par de límites cada vez más cercanos entre los cuales debía estar π.
Círculos con hexágonos afuera y adentro
No sabemos si los ciudadanos de Sicilia alguna vez vieron el cuerpo desnudo de Arquímedes, pero la verdad sobre la corona del rey fue revelada: el orfebre había sido deshonesto y Arquímedes había resultado ser un buen detective.
Durante su vida, Arquímedes se hizo famoso por sus inventos y temido por sus armas de guerra.
El rey lo nombró consejero militar y le encargó la defensa de la ciudad.
Pero es a través de sus matemáticas que se revela su verdadero genio.
3.14159265358979323846...
Fue a él a quien se le ocurrió un valor para π, vital para calcular el área de un círculo, uno de los componentes básicos de la ciencia.
Lo hizo valiéndose de polígonos, pues su perímetro se puede calcular dado que sus lados son rectos.
Comenzó poniendo un hexágono dentro del círculo y otro fuera. Luego, fue agregando más y más lados hasta tener 96.
La idea era hacer que los polígonos se acercaran cada vez más al perímetro del círculo, pues eso le daría un par de límites cada vez más cercanos entre los cuales debía estar π.
Círculos con hexágonos afuera y adentro
Para calcular π...
Así calculó que el valor de π estaba entre 310 ⁄ 71 (aproximadamente 3,1408) y 31 ⁄ 7 (aproximadamente 3,1429), una estimación que siguen utilizando los ingenieros hoy en día y es más que suficiente para todos los propósitos prácticos.
Obsesionado por las matemáticas, no había ningún problema demasiado ambicioso para Arquímedes.
Calculó hasta la cantidad de granos de arena para llenar el Universo.
La respuesta: 10, seguido de 62 ceros.
Los historiadores de su época contaban que Arquímedes se ponía eufórico cuando descubría formas matemáticas cada vez más complejas.
12 cuadrados, 8 hexágonos, 6 octágonos constituyen un cubeoctaedro truncado...
...12 pentágonos, 30 cuadrados y 20 triángulos, 60 vértices, 120 aristas, 62 caras: un rombicosidodecaedro...
... y más y más.
Obsesionado por las matemáticas, no había ningún problema demasiado ambicioso para Arquímedes.
Calculó hasta la cantidad de granos de arena para llenar el Universo.
La respuesta: 10, seguido de 62 ceros.
Los historiadores de su época contaban que Arquímedes se ponía eufórico cuando descubría formas matemáticas cada vez más complejas.
12 cuadrados, 8 hexágonos, 6 octágonos constituyen un cubeoctaedro truncado...
...12 pentágonos, 30 cuadrados y 20 triángulos, 60 vértices, 120 aristas, 62 caras: un rombicosidodecaedro...
... y más y más.

Mosaico romano de la época imperial representando la muerte de Arquímedes quien fue asesinado por un soldado romano en Siracusa.
El genio de Arquímedes lo hizo tan conocido que los romanos supieron de él, y ansiaban capturarlo para tenerlo en sus lares.
Cuando finalmente lograron invadir Siracusa se emitieron órdenes para tomar Arquímedes prisionero.
Tragicamente, el mensaje no le llegó a uno de los soldados.
Cuando lo encontró, completamente absorto en sus matemáticas, sin haberse siquiera percatado del alboroto a su alrededor, lo mató con su espada.
Un reciclaje devastador
La muerte de Arquímedes en 212 a.C. marcó el fin de una edad de oro en las matemáticas griegas, que fueron declinando gradualmente.
Sin embargo, las escrituras de Arquímedes sobrevivieron, copiadas por escribas que transmitieron sus preciosas ideas de generación en generación, hasta que en el siglo X se hizo una copia final de sus obras más importantes.
Pero el interés en las matemáticas se había perdido. El nombre de Arquímedes se había ido esfumando.
Un día del siglo XII un monje se quedó sin pergaminos. La consecuencia fue desastrosa.
Hecho mano a las páginas de esa copia final de la obra más importante de Arquímedes para reutilizarlas en un libro de oraciones.
Cada una de las hojas del manuscrito fueron cortadas, lavadas y raspadas hasta que quedaron lo suficientemente claras como para poder escribir sobre ellas.
El manuscrito fue reciclado y convertido en lo que se conoce como un palimpsesto (del griego palin: otra vez y psaein: grabar).
El resultado: un libro de oraciones del monasterio de Mar Saba en el desierto de Judea en Medio Oriente.
El renacer matemático
Cuando finalmente lograron invadir Siracusa se emitieron órdenes para tomar Arquímedes prisionero.
Tragicamente, el mensaje no le llegó a uno de los soldados.
Cuando lo encontró, completamente absorto en sus matemáticas, sin haberse siquiera percatado del alboroto a su alrededor, lo mató con su espada.
Un reciclaje devastador
La muerte de Arquímedes en 212 a.C. marcó el fin de una edad de oro en las matemáticas griegas, que fueron declinando gradualmente.
Sin embargo, las escrituras de Arquímedes sobrevivieron, copiadas por escribas que transmitieron sus preciosas ideas de generación en generación, hasta que en el siglo X se hizo una copia final de sus obras más importantes.
Pero el interés en las matemáticas se había perdido. El nombre de Arquímedes se había ido esfumando.
Un día del siglo XII un monje se quedó sin pergaminos. La consecuencia fue desastrosa.
Hecho mano a las páginas de esa copia final de la obra más importante de Arquímedes para reutilizarlas en un libro de oraciones.
Cada una de las hojas del manuscrito fueron cortadas, lavadas y raspadas hasta que quedaron lo suficientemente claras como para poder escribir sobre ellas.
El manuscrito fue reciclado y convertido en lo que se conoce como un palimpsesto (del griego palin: otra vez y psaein: grabar).
El resultado: un libro de oraciones del monasterio de Mar Saba en el desierto de Judea en Medio Oriente.
El renacer matemático
La ciencia había avanzado lo suficiente como para que los estudiosos comprendieran los argumentos matemáticos de Arquímedes, pero nadie tenía la menor idea de que se habían perdido algunas de sus ideas más brillantes.
Los matemáticos del Renacimiento tuvieron que lidiar con conceptos y problemas que Arquímedes había resuelto 1.500 años antes.
Pasaron cientos de años antes de que se volviera a saber del manuscrito.
Nadie sabe cómo, pero apareció en una biblioteca en Constantinopla.
Revisando el catálogo de la biblioteca, algo llamó la atención del experto danés en cultura griega Johan Ludvig Heiberg, así que fue a Constantinopla en 1906 para ver el documento que despertó su curiosidad.
Como no podía sacar el manuscrito de la biblioteca, Heiberg se llevó fotografías de las página y con ellas intentó reconstruir la obra de Arquímedes, una tarea increíblemente difícil cuando su única ayuda era una lupa.
Con todo y eso, descubrió que bajo las oraciones escritas por los monjes medievales pervivían los rastros de ideas nunca antes vistas.
Arquímedes no solo daba respuestas a sus cálculos, sino que había escrito sus pensamientos más íntimos, revelando cómo había llevado a cabo su trabajo.
Tituló la obra "El Método".
"Fue un hallazgo espectacular para la historia de las matemáticas.
"Si eres un pintor, seguramente estás interesado en los trabajos terminados de los Maestros, pero más que eso, querrás aprender las técnicas, los métodos, las pinturas que utilizaron. Así mismo, los matemáticos quieren saber no sólo cuáles fueron sus teoremas, sino cómo llegó a ellos", ilustró Rorres.
Escalas en la mente
Grabado que representa la concepción artística del matemático e inventor griego Arquímedes (c. 287-212 a. C.), sentado en una silla pensando

En su mente había construido un conjunto de escalas completamente imaginario para comparar los volúmenes de formas curvas. Lo usó para tratar de calcular el volumen de una esfera.
Como ya se conocía el volumen de un cono y un cilindro, trató de equilibrar la esfera y el cono en un lado con el cilindro en el otro.
Todo en su mente.
Imaginó hacer un número infinito de cortes y, usando una matemática muy compleja, encontró la forma de equilibrar los objetos en las escalas.
El resultado final: el volumen de una esfera es precisamente dos tercios del volumen del cilindro que encierra esta esfera.
Fue un resultado que consideró tan importante que pidió que lo inscribieran en su lápida como su descubrimiento matemático más importante.
Elaborar volúmenes utilizando infinitos cortes indica que Arquímedes estaba dando el primer paso hacia una rama vital de las matemáticas 1.800 años antes de que se inventara.
Se trataba del cálculo, aquello sin lo que el mundo moderno no podría existir. Es esencial para científicos e ingenieros, y de él depende la tecnología del siglo XXI.
Otra desaparición
En 1914, cuando estaba a punto de descubrir el verdadero genio de Arquímedes, la Primera Guerra Mundial estalló. Europa y el Medio Oriente se vieron sumidos en la confusión y el palimpsesto se perdió de nuevo.
Los académicos tenían pocas esperanzas de volver a ver el documento.
Pero en 1971, el británico Nigel Wilson, experto en Estudios Clásicos, oyó hablar de una página de un manuscrito en una biblioteca de la Universidad de Cambridge y fue a investigar.
"Transcribí algunas oraciones. Incluían algunos términos técnicos muy específicos. Por el léxico descubrí rápidamente que se trataba de un ensayo de Arquímedes, y me di cuenta de que debía ser una hoja del famoso palimpsesto", le contó a la BBC.
Página del libro de oraciones escrito sobre los textos de Arquímedes.

¿Pero por qué apareció en Cambridge una sola página del palimpsesto de Arquímedes?
Una pista era su proveniencia: era uno de una colección de documentos que había pertenecido a un erudito llamado Constantine Tischendorf, un hombre de pocos escrúpulos.
"Tischendorf viajó mucho en Medio Oriente. En Constantinopla visitó la biblioteca y dijo que sólo quedaba un manuscrito de interés: un palimpsesto con un texto matemático. No dijo más", apuntó Wilson.
"Suponemos que se robó esa página", añadió.
A principios del siglo XX, Heiberg sólo tenía una lupa para leer el manuscrito. En los años 70, Nigel Wilson tenía la ventaja de la tecnología moderna.
"La mayor parte de la página era legible y con la lámpara ultravioleta, las esquinas, que no se podían leer, se aclararon".
¡Si sólo supieran dónde estaba el resto del manuscrito!
Después de la Primera Guerra Mundial, París y otras ciudades europeas se inundaron de obras de arte de Medio Oriente, pero la obra de Arquímedes no aparecía.
En 1991, Félix de Marez Oyens, quien se convertiría en un distinguido experto, empezó a trabajar para la casa de subastas Christies.
En su nueva oficina encontró una carta de una familia francesa que decía tener un palimpsesto.
Intrigado, De Marez Oyens fue a examinarlo.
Expertos analizando el palimpsestoFuente de la imagen,Getty Images Pie de foto,
Cuando el Palimpsesto de Arquímedes llegó al Museo Walters de Baltimore se pudo por fin analizar con tecnología más moderna y ver lo antes oculto.
Una pista era su proveniencia: era uno de una colección de documentos que había pertenecido a un erudito llamado Constantine Tischendorf, un hombre de pocos escrúpulos.
"Tischendorf viajó mucho en Medio Oriente. En Constantinopla visitó la biblioteca y dijo que sólo quedaba un manuscrito de interés: un palimpsesto con un texto matemático. No dijo más", apuntó Wilson.
"Suponemos que se robó esa página", añadió.
A principios del siglo XX, Heiberg sólo tenía una lupa para leer el manuscrito. En los años 70, Nigel Wilson tenía la ventaja de la tecnología moderna.
"La mayor parte de la página era legible y con la lámpara ultravioleta, las esquinas, que no se podían leer, se aclararon".
¡Si sólo supieran dónde estaba el resto del manuscrito!
Después de la Primera Guerra Mundial, París y otras ciudades europeas se inundaron de obras de arte de Medio Oriente, pero la obra de Arquímedes no aparecía.
En 1991, Félix de Marez Oyens, quien se convertiría en un distinguido experto, empezó a trabajar para la casa de subastas Christies.
En su nueva oficina encontró una carta de una familia francesa que decía tener un palimpsesto.
Intrigado, De Marez Oyens fue a examinarlo.
Expertos analizando el palimpsestoFuente de la imagen,Getty Images Pie de foto,
Cuando el Palimpsesto de Arquímedes llegó al Museo Walters de Baltimore se pudo por fin analizar con tecnología más moderna y ver lo antes oculto.

Los propietarios dijeron que en la década de 1920, un pariente que era un coleccionista aficionado había adquirido el manuscrito en Constantinopla.
Ahora ellos querían venderlo.
¿Cuál es el precio de lo invaluable?
"Cualquier valoración de algo así es simplemente una suposición. Creo que les dije que valía entre US$550.000 y US$800.000", dijo De Marez Oyens.
Un multimillonario anónimo pagó, en 1998, US$2.000.000.
Gracias a que, unos meses después de comprarlo, el nuevo dueño depositó el manuscrito en The Walters Art Museum en Baltimore, Maryland, llegó por fin el momento de recuperar conocimientos perdidos durante más de dos milenios.
Científicos, conservadores, clasicistas e historiadores pusieron manos a la obra.
Utilizando tecnología como imágenes multiespectrales y una técnica de rayos X que hace brillar el hierro en la tinta que fue raspada, descubrieron que el documento no sólo contenía 7 tratados de Arquímedes, sino además discursos del orador ateniense clásico Hiperides y un comentario sobre las Categorías de Aristóteles del II o III siglo d.C.
Entre los tratados del matemático griego estaba la única copia sobreviviente del Ostomachion de Arquímedes, en el que trata de descubrir de cuántas maneras se pueden recombinar 14 piezas fijas para formar un cuadrado perfecto.
Ostomachion de Arquímedes
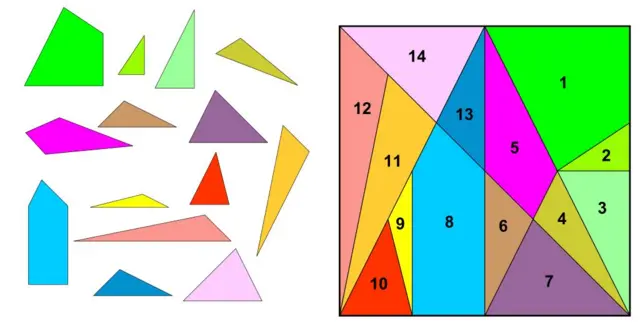
La respuesta es 17.152 combinaciones.
Se trata del primer trabajo para desarrollar la matemática de las combinaciones que es la base de las matemáticas de la probabilidad, algo que se pensaba había surgido en el siglo XVII o XVIII.
Hasta el infinito
Se trata del primer trabajo para desarrollar la matemática de las combinaciones que es la base de las matemáticas de la probabilidad, algo que se pensaba había surgido en el siglo XVII o XVIII.
Hasta el infinito
Notablemente, la lectura de El Método dejo claro que Arquímedes había dado un gran paso hacia la comprensión del infinito; más que eso, había usando el concepto como parte de un argumento en uno de los teoremas.
Arquímedes estaba aún más cerca de la ciencia moderna de lo que se creía.
Aunque ya se sabía que había dado algunos pasos en la dirección que conduce al cálculo moderno, el palimpsesto mostró que, en cierto sentido, no sólo había recorrido gran parte del camino, sino que tal vez ya había llegado.
¿Qué habría pasado, entonces, si ese documento no se hubiera perdido? ¿ O si al menos lo hubieran tenido los matemáticos del Renacimiento?
"Habría cambiado las matemáticas, por supuesto, pero hay que tener en cuenta que éstas influyen en todas las ciencias, así que básicamente habría sido como subir la marea del conocimiento varios cientos de años atrás", contestó Rorres.