"Respetado señor", empezaba diciendo una carta que recibió un día de junio de 1924 el para entonces ya premio Nobel y muy célebre Albert Einstein.
La misiva provenía de la Universidad de Daca, una ciudad que formaba parte de la India británica, así que estaba en la periferia colonial, lejos del centro científico del mundo en el que todo el conocimiento establecido se estaba revolucionando.
"Me he atrevido a enviarle el artículo adjunto para su lectura y opinión. Estoy deseoso de saber qué piensa al respecto. Si considera que el trabajo merece ser publicado, le agradecería que gestionara su publicación en Zeitschrift für Physik".
La alemana Zeitschrift für Physik (Revista de Física) era una de las publicaciones más importantes del mundo en física teórica y experimental de aquel entonces.
¿Quién era el autor de esa carta y qué lo había animado a formular una solicitud semejante? Revista de Física reconocía como "un completo desconocido" para Einstein, pero señalaba: "No siento ninguna vacilación en hacerle tal solicitud, pues todos somos discípulos suyos".
No obstante, revelaba que no era la primera vez que le escribía: "No sé si aún recuerda que alguien desde Calcuta le pidió permiso para traducir sus trabajos sobre la relatividad al inglés. Usted accedió a esa petición. El libro fue publicado. Yo fui quien tradujo su trabajo".
Y firmaba: "Atentamente, S. N. Bose".
Adjunto iba un artículo que el autor ya había enviado a la prestigiosa publicación de la Real Sociedad británica Philosophical Magazine, pero que pasaron por alto.
Afortunadamente no se dio por vencido: se requirió el genio y la perspicacia de Einstein para apreciar la importancia de dicho trabajo.
El físico y matemático Satyendra Nath Bose había encontrado la solución a un problema que ni siquiera Einstein había podido resolver.
En cuestión de ocho días, el maestro de la relatividad ya había traducido el artículo al alemán y lo había enviado para su publicación a la revista Zeitschrift für Physik, acompañado de una nota en la que lo calificaba como "un avance importante" y anticipaba que él mismo ampliaría esas ideas revolucionarias.
A Bose, le escribió una postal confirmándole que su trabajo era "un importante paso adelante", y agregando: "Me complace mucho".
Ese paso adelante se fue haciendo cada vez más enorme.
Foto de Bose
La misiva provenía de la Universidad de Daca, una ciudad que formaba parte de la India británica, así que estaba en la periferia colonial, lejos del centro científico del mundo en el que todo el conocimiento establecido se estaba revolucionando.
"Me he atrevido a enviarle el artículo adjunto para su lectura y opinión. Estoy deseoso de saber qué piensa al respecto. Si considera que el trabajo merece ser publicado, le agradecería que gestionara su publicación en Zeitschrift für Physik".
La alemana Zeitschrift für Physik (Revista de Física) era una de las publicaciones más importantes del mundo en física teórica y experimental de aquel entonces.
¿Quién era el autor de esa carta y qué lo había animado a formular una solicitud semejante? Revista de Física reconocía como "un completo desconocido" para Einstein, pero señalaba: "No siento ninguna vacilación en hacerle tal solicitud, pues todos somos discípulos suyos".
No obstante, revelaba que no era la primera vez que le escribía: "No sé si aún recuerda que alguien desde Calcuta le pidió permiso para traducir sus trabajos sobre la relatividad al inglés. Usted accedió a esa petición. El libro fue publicado. Yo fui quien tradujo su trabajo".
Y firmaba: "Atentamente, S. N. Bose".
Adjunto iba un artículo que el autor ya había enviado a la prestigiosa publicación de la Real Sociedad británica Philosophical Magazine, pero que pasaron por alto.
Afortunadamente no se dio por vencido: se requirió el genio y la perspicacia de Einstein para apreciar la importancia de dicho trabajo.
El físico y matemático Satyendra Nath Bose había encontrado la solución a un problema que ni siquiera Einstein había podido resolver.
En cuestión de ocho días, el maestro de la relatividad ya había traducido el artículo al alemán y lo había enviado para su publicación a la revista Zeitschrift für Physik, acompañado de una nota en la que lo calificaba como "un avance importante" y anticipaba que él mismo ampliaría esas ideas revolucionarias.
A Bose, le escribió una postal confirmándole que su trabajo era "un importante paso adelante", y agregando: "Me complace mucho".
Ese paso adelante se fue haciendo cada vez más enorme.
Foto de Bose

De la breve pero significativa colaboración entre Einstein y Bose brotaron conocimientos pioneros en la ciencia cuántica que siguen transformando el mundo.
Pero a pesar de haber contribuido a cambiar el rostro de la ciencia del siglo XX y, además, haber trabajado con Marie Curie, inspirado al poeta Tagore y frecuentado a grandes científicos y artistas, el físico indio es poco conocido.
Y es un gusto conocerlo.
110 sobre 100
Bose nació el primer día del año 1894 en Calcuta, en el seno de una familia vinculada al Renacimiento bengalí, un movimiento que impulsaba la educación moderna y la renovación cultural en la India colonial.
Desde muy temprano brilló por su intelecto.
Entre las varias historias que circulan sobre su genio -algunas reales y otras quizá adornadas-, se cuenta que un profesor de su escuela, impresionado por uno de sus trabajos, le otorgó una calificación de 110 sobre 100.
El maestro estaba convencido de que su estudiante llegaría a ser un matemático brillante.
Bose, siempre curioso por todo tipo de creación intelectual y artística, efectivamente acabó inclinándose por las matemáticas como su camino profesional.
Y, así como a su amigo, compañero de estudios y futuro astrofísico Meghnad Saha, le fascinaba la física teórica, especialmente la nueva teoría cuántica que los físicos alemanes estaban explorando.
Tras graduarse y convertirse en profesores en la Universidad de Calcuta, Bose y Saha se lanzaron a una tarea inusual: traducir al inglés los trabajos originales de Einstein y Hermann Minkowski sobre relatividad, algo que no se había hecho en ningún lugar antes.
¿Recuerdas que en su carta a Einstein Bose mencionó que ya le había escrito antes?
Pues esta fue la razón: para no violar los derechos de autor del gran físico, le solicitó un permiso especial.
Einstein se lo otorgó gustosamente y el libro The Principle of Relativity, publicado en 1920, fue la primera colección en inglés de esos artículos fundamentales.
Más que una simple traducción, fue un puente hacia el conocimiento global, un gesto que facilitó la difusión de ideas revolucionarias en una época en que las noticias científicas tardaban mucho en cruzar fronteras.
Foto de la boda coloreada

Sin embargo, fue cuando Bose se mudó de Calcuta a la Universidad de Dakar que realmente hizo historia, con ese artículo titulado "La ley de Planck y la hipótesis cuántica de la luz" que le envió a Einstein.
Fue como una llave que abrió la puerta a conocimientos.
En paralelo y gracias a Einstein, Bose obtuvo una licencia de investigación para viajar a Europa y trabajar con los mejores laboratorios e investigadores de la época.
El gracioso encuentro con Marie Curie
Bose llegó a París en octubre de 1924 y rápidamente se introdujo en los círculos científicos, asistiendo a conferencias y charlas de figuras como los físicos Paul Langevin y Louis de Broglie.
Interesado en aprender técnicas experimentales de radioactividad, Langevin le proporcionó una carta de presentación para conocer a Marie Curie en el Radium Institute.
Bose relató que, tras saludarlo "con cariño", ella le dijo: "Sin duda tendrás la oportunidad de trabajar conmigo, pero no ahora mismo, sino dentro de tres o cuatro meses. Primero tienes que aprender el idioma; de lo contrario, te resultará difícil desenvolverte en el laboratorio".
"Me dijo que debía conocer a una hermosa francesa de la que debía aprender. Así que buscamos por París a esa mujer tan guapa. La verdad es que yo sabía francés: sabía leer y escribir, pero no pude decírselo a madame Curie porque hablaba sin parar".
A Bose todo el episodio le pareció humorístico y, mientras esperaba la oportunidad de integrarse formalmente en el laboratorio de Curie, aprovechó su estancia en París para trabajar con otros investigadores y familiarizarse con técnicas punteras de la física experimental.
Entre ellos se encontraba la física francesa Jacqueline Zadoc-Kahn Eisenmann, con quien entabló una profunda amistad.
La correspondencia entre ambos retrata los vibrantes intercambios intelectuales de la física cuántica de la época, como ilustra esta carta que Bose le escribió ya desde Berlín, en 1925:
«Mi dulce Jacqueline, tu rápida respuesta me dio alegría, pero mezclada con ella hay una sensación de tristeza: me hace pensar en lo poco que te vi el último día.
»Parece que todo el mundo en Berlín está muy entusiasmado con la evolución de la física.
»El día 1 y el 28 del mes pasado, [Werner] Heisenberg habló en el coloquio sobre su teoría. Todo el mundo está muy desconcertado, y muy pronto habrá una discusión sobre los trabajos de [Erwin] Schrödinger.
»Einstein parece muy entusiasmado con ello. El otro día, al volver del coloquio en tren, lo encontramos saltando al mismo compartimento en el que estábamos nosotros, y enseguida empezó a hablar con pasión sobre lo que acabábamos de oír.
»Todos guardabamos silencio, mientras él hablaba casi todo el tiempo, sin advertir el interés y la fascinación que despertaba en los demás pasajeros».
De vuelta en casa

Cualquier físico que visitara Berlín en los años 20 debió sentirse un poco como un músico que visitaba Liverpool en los años 60, comentó la física y escritora de ciencia Sharon Ann Holgate en el retrato radial de Bose de la BBC The Indian Particle Man.
Algunas de las mentes más brillantes de principios del siglo XX estaban ahí discutiendo sobre los entresijos de la extraña nueva teoría cuántica que parecía casi demasiado extraña para comprender.
"Nunca en tu vida tendrás la oportunidad de conocer a hombres tan grandes de la ciencia", señaló Bose.
Pero India y su familia lo esperaban.
A su regreso, Bose se consolidó como una figura central de la física del país, combinando docencia, investigación y liderazgo institucional, e influyendo en generaciones de científicos.
Algo que defendió con firmeza fue la importancia de la enseñanza de la ciencia en las lenguas nativas de India, en lugar del inglés.
Según contó a la BBC su nieto, Falguni Sarkar, Bose admiraba a países como Israel y Japón por haber logrado crear una cultura científica sólida y contribuciones de primer nivel basadas en el uso de los idiomas propios.
La idea, sin embargo, encontró mucha resistencia. El físico indio Partha Ghose, discípulo de Bose, recordó que un día le preguntó por qué insistía tanto en esa cuestión, y que recibió una respuesta "muy convincente".
"No pienso en personas como tú, que se dedican a la ciencia -le dijo Bose-. Pienso en el indio medio: ¿por qué tendría que aprender un idioma extranjero para poder comprender las cosas básicas que ocurren en la ciencia?".
Bose tocando el esraj ante un público de varios hombres

Su actividad no se limitó a la ciencia: fue también un intelectual humanista, profundamente interesado por la música -en particular la música clásica india-, la literatura y el arte, y participó activamente en los círculos culturales de su tiempo, convencido de que la creatividad científica formaba parte de un impulso creativo más amplio.
Pero volvamos a la creatividad científica de Bose y Einstein, y a ese artículo.
La brillantez de Bose
A finales del siglo XIX, los físicos se enfrentaban a un problema aparentemente sencillo: cómo emite luz un objeto caliente. Más exactamente, cuánta luz emite en cada color según su temperatura. Si se calienta un metal, ¿cuánta luz roja produce?, ¿cuánta azul?, ¿cómo cambia ese reparto al aumentar la temperatura?
La física clásica intentó responder usando las leyes conocidas del electromagnetismo y la termodinámica… y fracasó estrepitosamente.
Sus ecuaciones predecían que un cuerpo debería emitir una cantidad infinita de radiación ultravioleta, algo que claramente no ocurría. A ese absurdo teórico se lo bautizó, con cierta ironía, como la catástrofe ultravioleta.
El problema era profundo: no se trataba de un error experimental, sino de una contradicción interna de la teoría. Las mismas leyes que describían con éxito el mundo cotidiano conducían aquí a un sinsentido matemático.
Entender cómo emite luz un cuerpo caliente no era un detalle técnico menor, sino una señal de que algo fundamental fallaba en la forma misma de concebir la energía y la radiación.
Resolverlo exigía cambiar las reglas del juego.
Cartas escritas por Satyendra Nath Bose (izquierda) y Albert Einstein (derecha) sobre las estadísticas de Bose.

En 1900, el físico alemán Max Planck resolvió el enigma proponiendo algo radical para la época: la energía no se intercambiaba de manera continua, sino en pequeños "paquetes" o cuantos, cuyo tamaño dependía de la frecuencia de la radiación.
Su fórmula describía con precisión cómo emiten luz los objetos según su temperatura.
Lo verdaderamente profundo no fue solo que funcionara, sino lo que implicaba: la energía estaba cuantizada. Esa ruptura con la física clásica abrió la puerta justamente a la física cuántica.
Unos años más tarde, Einstein llevó la idea un paso más allá y la aplicó directamente a la luz, proponiendo que la propia radiación viajaba en cuantos -los fotones- para explicar fenómenos que la teoría clásica no podía.
Aun así, la nueva física avanzaba sobre cimientos conceptuales todavía inestables. La ley de Planck funcionaba a la perfección, pero su justificación teórica seguía siendo insatisfactoria, apoyada en supuestos heredados de la física clásica que resultaban cada vez más frágiles.
Fue ahí donde Bose cambió radicalmente el enfoque.
Trató la luz no como una onda continua, sino como un conjunto de cuantos indistinguibles, y contó sus posibles distribuciones sin recurrir a los artificios conceptuales de la física clásica.
El resultado fue tan simple como contundente: la ley de Planck emergía de manera natural, sin parches ni contradicciones.
Con ello, Bose no solo aclaró el fundamento de una de las fórmulas más importantes de la física moderna, sino que mostró que la hipótesis de los cuantos de luz no era un recurso provisional, sino una pieza central de una nueva forma de entender la naturaleza.
La genialidad de Einstein
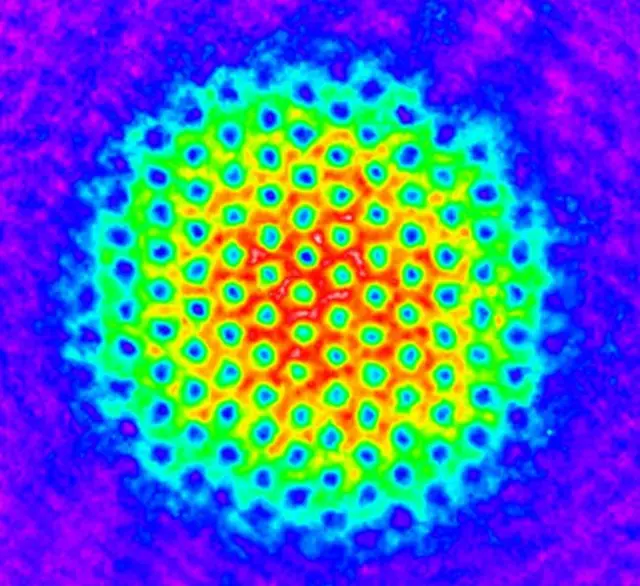
Una red coloreada de vórtices similares a tornados dentro de un condensado de Bose-Einstein giratorio de átomos de rubidio.
Einstein lo comprendió de inmediato.
Vio que Bose no había hecho un truco matemático, sino que había descubierto una nueva manera de contar, una forma inédita de describir sistemas formados por partículas indistinguibles.
Y aquí vino el giro sorprendente.
Einstein se preguntó: si esta forma de contar funciona para la luz, ¿qué ocurre si se aplica a la materia?
Al hacerlo, predijo algo completamente inesperado: que a temperaturas extremadamente bajas una gran cantidad de partículas podía colapsar en un mismo estado cuántico, comportándose como un único objeto macroscópico.
Así nació, al menos sobre el papel, el condensado de Bose-Einstein, conocido popularmente como el quinto estado de la materia.
Pasaron casi siete décadas antes de que los científicos confirmaran experimentalmente la predicción de Einstein.
Hoy, las ideas de Bose y Einstein sustentan tecnologías de vanguardia: desde computadoras cuánticas hasta imanes superconductores utilizados en resonancias magnéticas y los grandes aceleradores de partículas del CERN.
Incluso las matemáticas de la superconductividad inspiraron las ideas que llevaron a descubrir la partícula de Higgs y su papel en la estructura del universo.
Aunque muchos de los descubrimientos inspirados en este marco teórico obtuvieron Premios Nobel, el propio Bose no recibió tal galardón. Su legado, sin embargo, permanece inmortal en la física.
Su apellido dio origen al nombre de los bosones, una de las dos grandes familias de partículas fundamentales, formado a partir de "Bose" y el sufijo griego "-on", habitual en la nomenclatura subatómica.
En palabras del eminente físico y biógrafo de Einstein, Abraham Pais (1982): "El artículo de Bose es el cuarto y último de los artículos revolucionarios de la antigua teoría cuántica; los otros tres son de Planck, Einstein y Bohr".
¡Nada menos que la crema y nata de la física que transformó nuestro mundo!